不同沟形金刚石钻头刚度和强度的有限元分析

(a) 螺旋槽金刚石钻头

( b) 直槽金刚石钻头
图1 金刚石钻头三维模型
螺旋槽钻头建模参数为: 钻头直径D = 4.6mm,顶角2ø= 120º, 外缘后角af= 13º, 横刃斜角ø=55º, 沟槽螺旋角ß= 18º- 30º, 钻芯厚度dc =0.23D0.87= 0.87mm, 螺旋槽长L1= 40mm- 55mm, 钻头总长度L = 80mm。
直槽金刚石钻头建模参数为: 钻头直径D =4.6mm, 顶角2ø= 135º, 后角af= 13º, 横刃斜角ø=55º, 钻芯厚度dc= 0.23D0.87= 0.87mmmm, 沟槽长度L1= 40mm, 钻头总长L = 80mm。
2. 2 单元网格划分及材料属性定义
将Pro/ E 建立的金刚石钻头三维模型导入有限元分析软件ABAQUS 中, 对其进行网格划分。其中钻体部分的单元类型采用C3D4 线性三维应力四面体单元, PCD 刀片采用C3D8R 显式线性三维应力六面体单元, 并对刀片部分的网格进行密化处理, 刀片单元网格数为7968, 钻体部分单元网格数为11246,如图2 所示。金刚石钻头刀体和PCD 刀片的材料属性如表1 所列[6] 。

(a) 螺旋槽金刚石钻头
( b) 直槽金刚石钻头
图2 金刚石钻头单元划分
表1 金刚石钻头的材料属性
2. 3 载荷分布及边界条件
(1) 钻削力分布
在钻削加工过程中, 钻削力主要来自于主切削刃、横刃和副刃, 可以合成为一个总的轴向力Fz 和一个扭矩T, 各切削刃上的轴向力和扭矩分布如图3所示[1- 5], 总轴向力和扭矩在各切削刃上的分配比例[3] 见表2。
材料
高速钢
PCD
密度( g/ cm3)
8. 3
4.1
弹性模量(GPa)
210
800
泊松比
0.25
0.07
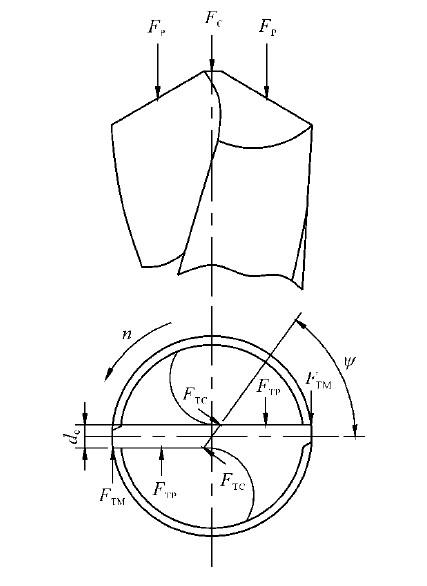
图3 钻削力分布
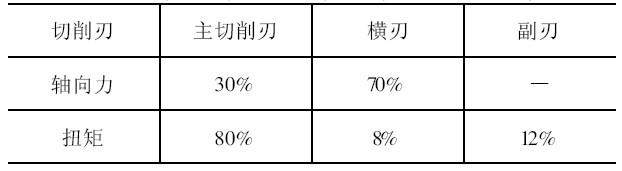
表2 钻头切削刃上轴向力和扭矩的分配比例
轴向力Fz 主要分布在钻头横刃和两条主切削刃上, 在有限元计算时根据静力等效原则, 将轴向力Fz 等效为分布在横刃和两条主切削刃上各节点的集中载荷。把钻头受到的扭矩T 转化为切向力施加于主切削刃、横刃及副刃上; 两条主切削刃上的切向力等效为分布在各节点的集中载荷, 这些集中载荷由钻芯至边缘呈线性分布[ 3] ; 由于钻头横刃很短, 假定横刃上的切向力作用于横刃两个端点处; 副刃上的切向力作用于钻头边缘处。
计算时按照钻削力的分布情况在切削刃上施加相应载荷, 其中扭矩是通过在切削刃上施加环向力实现。分别改变螺旋槽金刚石钻头的钻芯厚度、刃沟螺旋槽角度、螺旋槽长度, 查看计算结果u、v 、w( 分别为钻头各节点沿x、y、z方向的最大位移) , 并按式( 1) [ 2] 将u、v 、w 转化为最大径向位移R 、角位移及轴向位移z , 分别代表了钻头的弯曲刚度、扭转刚度和轴向抗压刚度。
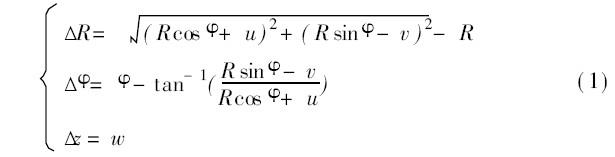
式中, 为钻头切削刃上任一节点的转角, R 为切削刃上任一节点的半径。
( 2) 边界条件
钻削过程中, 金刚石钻头柄部装夹在机床主轴的夹具中, 有限元计算时对柄部装夹部分( 长度约为15mm) 约束其所有自由度; 在刀片与刀体之间使用Tie 约束, 使二者直接应力应变等可以传递, 并且二者之间不会有大变形、大位移产生。
3 计算结果分析
3. 1 螺旋槽与直槽金刚石钻头应力及刚度分析
图4 所示为在相同载荷作用下, 螺旋槽和直槽金刚石钻头的等效应力云图。可以看出两种钻头的等效应力均产生在横刃及主切削刃处, 而直槽金刚石钻头的等效应力较大, 说明在同等条件下直槽金刚石钻头更容易因为受到较大应力而发生破损。
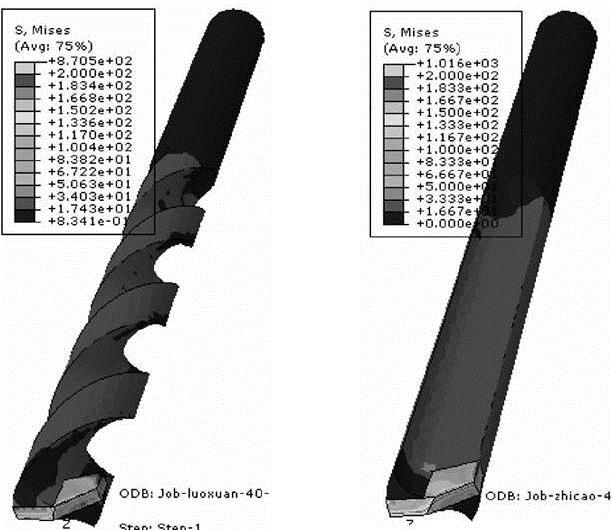
图4 螺旋槽与直槽金刚石钻头等效应力图
图5 所示为螺旋槽和直槽金刚石钻头的位移云图, 从图中数值可知直槽金刚石钻头总位移比螺旋槽的小。且通过x 、y 两个方向的位移计算出两种钻头的角位移分别为1.4º和0.87º, 直槽金刚石钻头的扭转角度小, 说明直槽金刚石钻头的抗扭刚度比螺旋槽的大。若是加工颗粒增强铝基复合材料等这类硬脆性材料, 直槽金刚石钻头比螺旋槽金刚石钻头更加适宜。
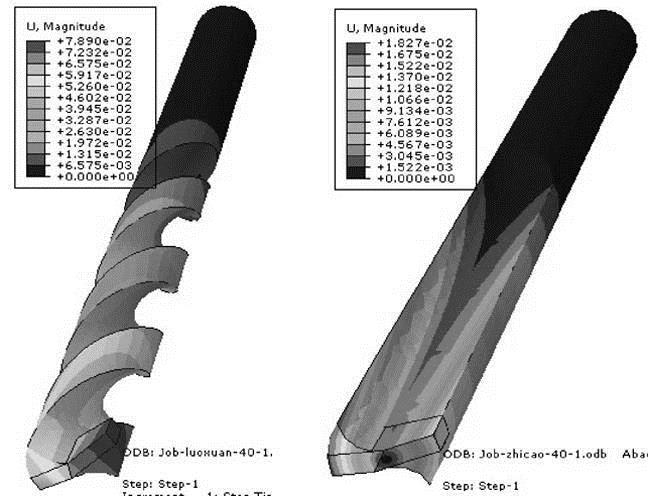
图5 螺旋槽与直槽金刚石钻头位移云图
3. 2 不同径向截形的螺旋槽金刚石钻头的刚度和强度分析
图6 是采用Pro/ E 建立的相同钻芯厚度, 不同径向截形的两种金刚石钻头模型的端面图, 建模尺寸为钻头直径D= 4.6mm, 沟槽螺旋角ß= 30º, 螺旋槽长度L1= 47mm, 钻芯厚度d c= 087mm, 顶角2= 120º。通过模拟钻削过程中钻头受力情况对两种截形金刚石钻头进行分析计算, 得到其等效应力云图和位移云图如图7、图8 所示。
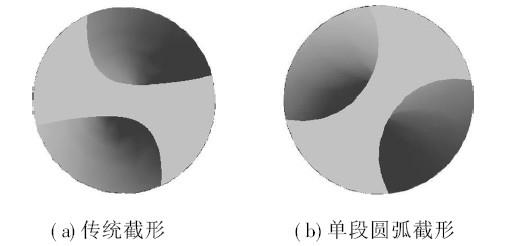
图6 金刚石钻头的两种径向截形端面图

图7 两种截形金刚石钻头的等效应力云图
从图中可以看出钻头受到的应力主要集中在横刃及主切削刃处, 且横刃处应力最大, 是金刚石钻头最容易损坏的部位, 两种截形金刚石钻头的最大等效应力比较接近, 其中传统截形的最大等效应力略小于单段圆弧截形。两种截形金刚石钻头的最大位移相差不大, 查看计算结果并通过式( 1) 得出其最大径向位移R 、最大轴向位移z 及最大角位移。如表3 所示。

图8 两种截形金刚石钻头的位移云图
表3 不同径向截形所对应的最大位移

从表3 可以看出相同载荷作用下, 传统径向截形与单段圆弧径向截形金刚石钻头的最大扭转角分别为3.073º和2.867º, 说明单段圆弧截形金刚石钻头的抗扭刚度稍好。而二者的最大轴向位移和径向位移相差并不大, 表明两种径向截形金刚石钻头的弯曲刚度和轴向抗压刚度相差不大。传统截形最大轴向位移略小, 抗压刚度较好, 这是由于传统截形钻头的有效截面面积较大, 但是有效截面面积越大表明钻头的容屑排屑空间越小, 即传统截形金刚石钻头的容屑排屑空间比单段圆弧径向截形的小。
3. 3 不同结构参数的螺旋槽金刚石钻头刚度分析
(1) 钻芯厚度对金刚石钻头刚度的影响
表4 所列为不同钻芯厚度所对应的钻头最大径向位移R 、最大轴向位移z 及最大角位移值。
表4 不同钻芯厚度所对应的最大位移

可以看出随着钻芯厚度的增加, 金刚石钻头的径向位移、轴向位移和角位移均减小, 说明钻芯厚度越大, 钻头的刚度越好。但是随着钻芯厚度的增加,钻头的容屑空间减小, 排屑难度增加, 会导致大量切屑堆积在钻头排屑槽内, 加剧钻头的磨损, 降低钻头的使用寿命和加工质量; 另外钻芯厚度的增加意味着横刃长度的增加, 将导致横刃切削条件变差, 特别是金刚石钻头, 其PCD 刀片具有硬脆性, 若横刃过长, 会导致轴向力的增大, 增加了刀片在钻削中的破损概率, 因此金刚石钻头不宜过度增加钻芯厚度。
(2) 螺旋角对金刚石钻头刚度的影响
不同螺旋角所对应的最大径向位移R 、轴向位移z 及角位移如表5 所示。
表5 不同螺旋角所对应的最大位移
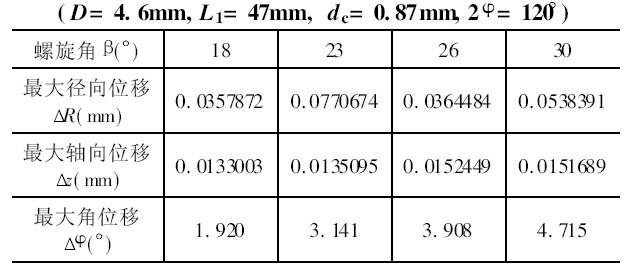
从表5 可以看出, 随着螺旋角的增大金刚石钻头的最大角位移增加, 扭转刚度下降。由于金刚石钻头前角为零度, 螺旋角对切削刃并无影响, 大的螺旋角有利于切屑的排出, 可减少因为切屑积存于排屑槽内导致钻头失效的可能性。而螺旋角过大, 则会增长排屑路程和排屑阻力, 若排屑不顺畅, 切屑也会堆积在排屑槽内, 还会导致散热条件变差, 金刚石钻头的PCD 刀片在高温下容易石墨化; 另外虽然金刚石刀具在加工中产生的切削力较小, 但是过大的螺旋角度仍然会使金刚石钻头的扭转刚度及抗压强度降低, 因此金刚石钻头螺旋角在排屑顺畅的情况下可选择稍大的螺旋角。
(3) 螺旋槽长度对金刚石钻头刚度的影响
表6 为不同螺旋槽长度所对应的最大径向位移R、轴向位移z 和角位移值。
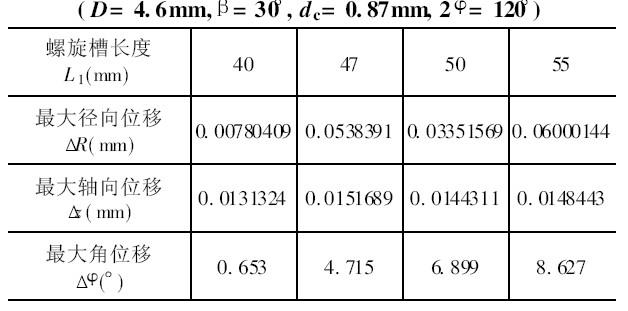
从表6 可以看出, 随着螺旋槽长度的增加, 钻头的最大角位移明显增大, 即钻头螺旋槽长度的增加会导致钻头的扭转刚度下降。为增加金刚石钻头的扭转刚度, 提高孔的加工质量, 应该尽可能选择较短的螺旋槽长度。
4 结语
(1) 直槽金刚石钻头的抗扭刚度比螺旋槽的高,但切削刃及横刃处的最大等效应力也较大; 单段圆弧截形金刚石钻头的抗扭刚度比传统截形的高。但切削刃及横刃处的最大等效应力比传统截形的略大。
( 2) 加厚钻芯可以提高钻头的抗弯、抗扭及抗压刚度, 但是加大钻芯厚度会带来较大的负面影响, 特别是金刚石钻头不宜使用较厚的钻芯。
(3) 减小螺旋槽角度和螺旋槽长度可以提高钻头的金刚石钻头抗扭刚度, 但过小的螺旋角会影响切屑的顺利排出, 确定合理的金刚石钻头结构参数
(4) 金刚石钻头所受应力主要集中在横刃及主切削刃处, 且横刃处应力最大, 是金刚石钻头最容易损坏的部位, 这与实际加工过程中的情况一致。
参考文献
[1] 谢大刚, 赵清亮, 袁哲俊, 等. 麻花钻刚度的有限元分析[J] . 中国机械工程, 2001( 5) : 154- 156.
[2] 言兰, 周志雄. 微钻头刚度的有限元分析[J] . 工具技术,2006( 4) : 64- 67.
[3] 刘小川, 张平宽. 采用Pro/ E 和ANSYS 的微小钻头的刚度分析[J] . 现代制造工程, 2008( 8) : 69- 71.
[4] Chen Wenchou. Applying the finite element rnethod to drill design based on drill deformations[J] . Finite Elements in Analysis and Design, 1997(26) : 57- 81.
[5] 董丽华, 刘大昕. 钻削力模型的建立及仿真[J] . 机械工程师, 2003(7) : 27- 30.
[6] 刘志强. PCD 刀具的金刚石砂轮机械刃磨工艺[J] . 工具技术, 2006(9) : 62- 64.第一作者: 许立福, 副教授, 沈阳理工大学机械工程学院, 110159 沈阳市First Author: Xu Lifu, Associate Professor, School of Mechanical Engineering, Shenyang Ligong University, Shenyang 110159, China